Python递归绘制科赫雪花

发表于 分类于 阅读次数： 阅读次数：

递归

递归的定义

递归通常指：函数定义中调用函数自身的方式。

也就是说，我们在定义函数的时候，函数的内部调用了它自己。

1
2
3
# 伪代码
def func():
    func()

电影《盗梦空间》本质就是递归：主角在做梦，梦的内容是自己在做梦，梦的内容是自己在做梦……

递归具有两个关键特征：

  1. 链条：计算过程存在递归链条
  2. 基例：存在一个或多个不需要再次递归的基例

类似于数学归纳法：假设n(k)成立，证明n(k+1)成立。

递归的调用过程

这里我们使用一个小栗子，它就是阶乘。

什么是阶乘呢？这里有一个阶乘的定义：

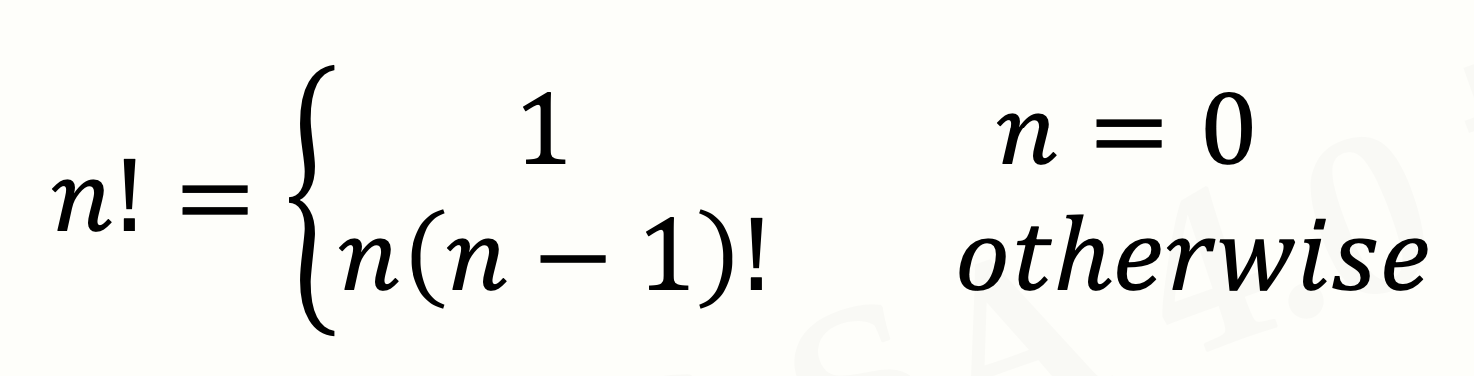
阶乘的定义中，又出现了阶乘本身。这就是递归。

我们编写一个函数来求任意一个数的阶乘：

1
2
3
4
5
def fact(n):
    if n == 0:
        return 1
    else:
        return n * fact(n - 1)

由此我们可以总结出：

  • 递归本身是一个函数，需要函数定义方式描述
  • 函数内部需要用分支语句对参数进行判断
  • 对基例和链条，分别编写对应代码

下面我们来看一个经典数列——斐波那契数列。

斐波那契数列又叫“兔子数列”，它指的是这样一个数列：

1
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144...

从第3项开始，每一项都是前边挨着两项的和。它的定义就是：

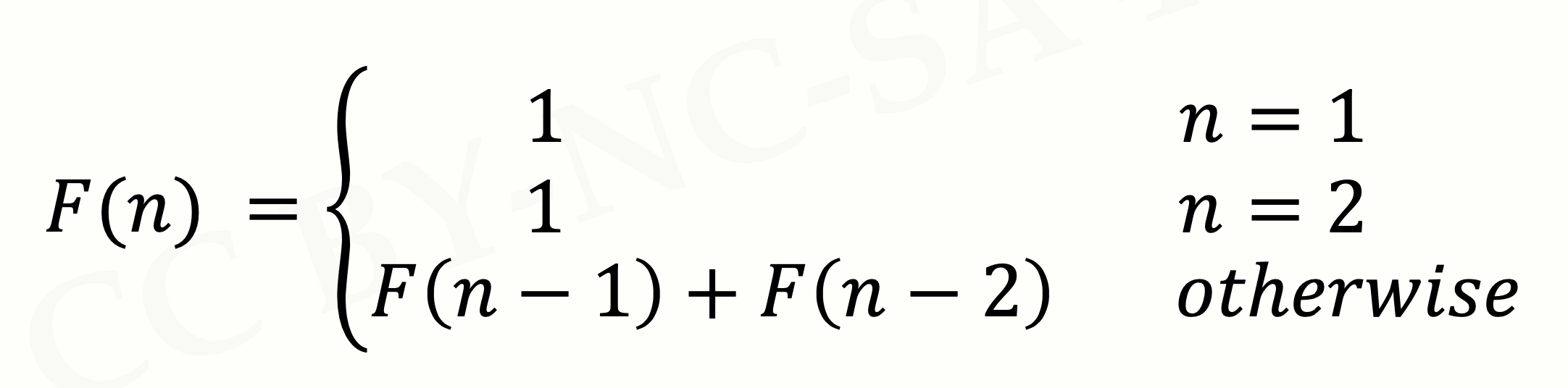
很容易理解，这个定义中的n=1和n=2的情况是基例，而F(n)=F(n-1)+F(n-2)是链条。这样我们可以编写一个函数，求出斐波那契数列的第n项。

1
2
3
4
5
def fib(n):
    if n == 1 or n == 2:
        return 1
    else:
        return fib(n - 1) + fib(n - 2)

接下来，我们可以循环打印一下数列的前几项。

1
2
for i in range(1, 15):
    print(fib(i), end=" ")

结果如下：

1
1 1 2 3 5 8 13 21 34 55 89 144 233 377

如果加入海龟绘图，还可以直接绘制出斐波那契曲线：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import turtle


def fib(n):
    if n == 1 or n == 2:
        return 1
    else:
        return fib(n - 1) + fib(n - 2)


turtle.seth(180)
for i in range(1, 15):
    turtle.circle(fib(i), 90)
    print(fib(i))

turtle.done()

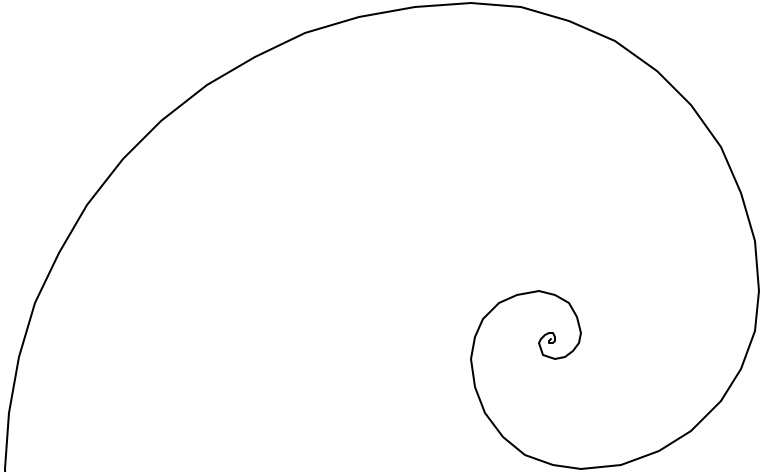
科赫曲线

分形几何

在大自然中，有很多植物的形状是局部的自己在复制整体的自己。

科赫曲线

科赫曲线是指这样一种曲线：当阶数为0时，科赫曲线是一条直线；当阶数不为0时，科赫曲线是一种带凸起的曲线。

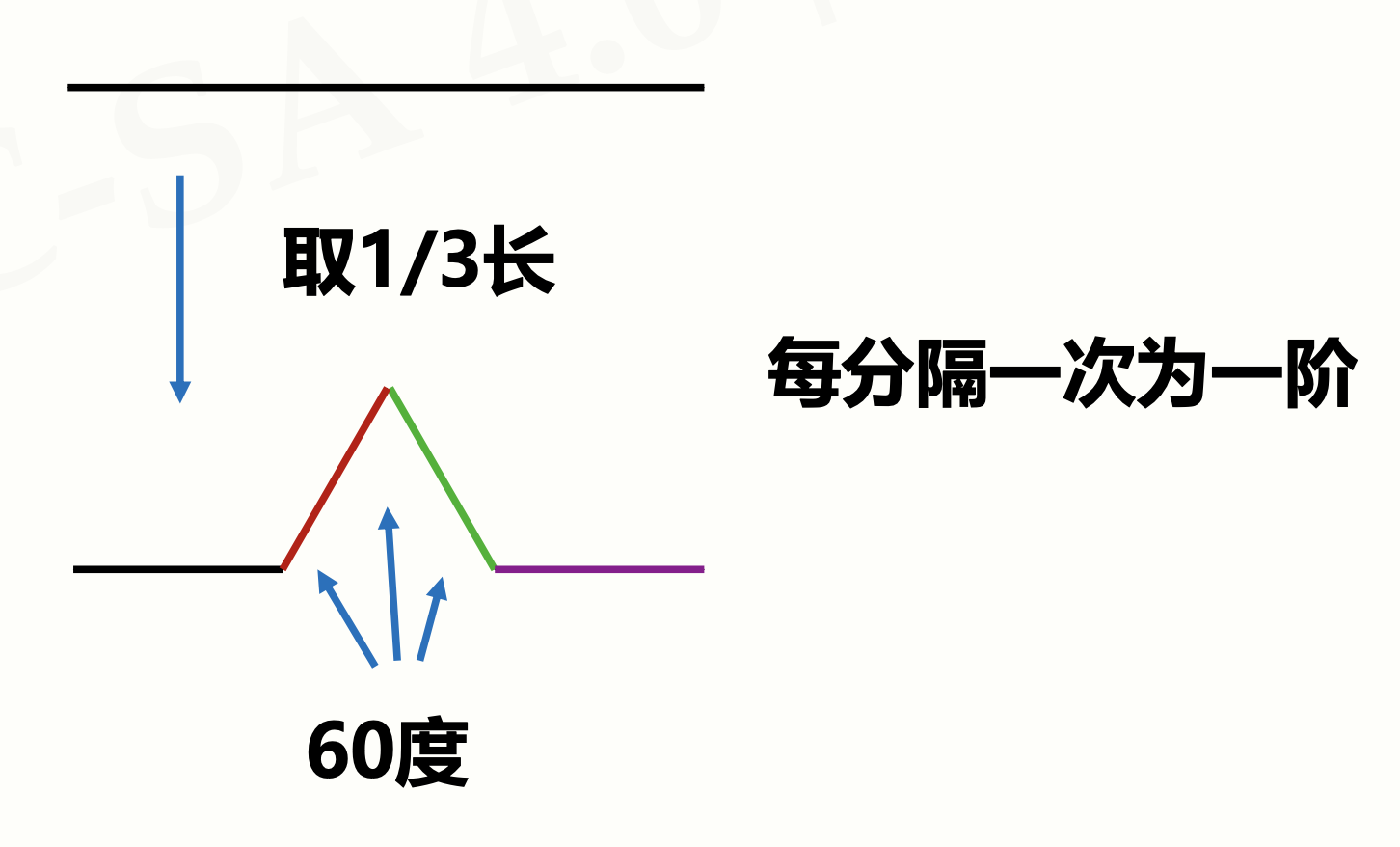
科赫曲线具有阶数，每一阶都会将上一阶的所有线段做一次变换。

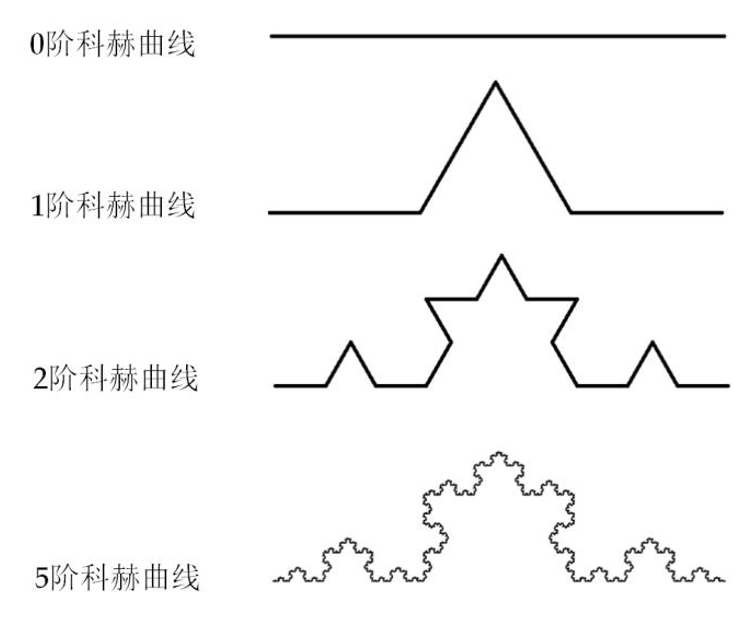
因此我们定义一个函数def koch(size, n)，得出它的的基例和链条：

  • 基例：n=0时，绘制一条直线
  • 链条：n≠0时，对n-1阶的每一条线段都做一次变换
1
2
3
4
5
6
7
8
9
10
11
12
def koch(size, n):  # size是初始线段长度
    if n == 0:
        turtle.fd(size)
    else:
        turtle.lt(0)
        koch(size / 3, n - 1)
        turtle.lt(60)
        koch(size / 3, n - 1)
        turtle.rt(120)
        koch(size / 3, n - 1)
        turtle.lt(60)
        koch(size / 3, n - 1)

将重复的代码改为for循环，右转改为左转：

1
2
3
4
5
6
7
8
9
10
import turtle


def koch(size, n):
    if n == 0:
        turtle.fd(size)
    else:
        for angle in [0, 60, -120, 60]:
            turtle.lt(angle)
            koch(size / 3, n - 1)

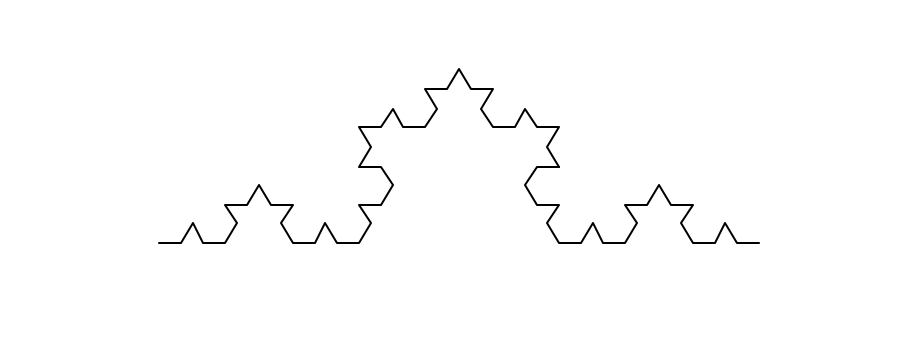
调用该函数koch(300, 3)，绘制一段3阶科赫曲线如下：

科赫雪花

其实掌握了科赫曲线，科赫雪花绘制就比较简单，只要将科赫曲线重复3次即可拼成一个雪花的形状。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
turtle.pu()
turtle.goto(150, 120)
turtle.pd()

turtle.bgcolor('skyblue')
turtle.color('white')

# 绘制雪花主体
turtle.begin_fill()
for i in range(3):
    turtle.rt(120)
    koch(300, 3)
turtle.end_fill()

turtle.hideturtle()
turtle.done()

画完的效果就是头图啦~

转自嵩天老师的课程《Python语言程序设计》- https://www.icourse163.org/course/BIT-268001